The Science of Math

What is the Science of Math?

You may have heard of the Science of Reading… now let’s talk the Science of Math.

I like to start these discussions with what we know about literacy, then parallel it to math, for two reasons:

• Literacy is much farther ahead than math in terms of research and development of what effective instruction is.
• Most people are much more familiar and comfortable with reading than they are with math.

For both these reasons, starting with literacy gives us a helpful foundation for understanding what effective numeracy instruction might be. 

What is the Science of Reading?

A web search on the Science of Reading describes it as “a body of research, spanning multiple disciplines, that investigates how children learn to read and provides evidence-based guidance for effective reading instruction, focusing on foundational skills like phonemic awareness and phonics.”

Deeper exploration into the Science of Reading makes the case that we need to pull from not just education research, which generally focuses on pedagogy and materials, but also neuroscience, psychology, and linguistics (see UFLI video). 

I would say the same goes for math.

My Journey into Math Research

I went into this research review thinking that the way research works is that “someone out there” does extensive research on a topic like teaching math, discovers what methods worked best, then develops those discoveries into instructional methods, and that’s how we found effective instruction. 

What I realized is that it’s quite the opposite. Research on a particular instructional method doesn’t exist until someone decides to do a study on it. So the methods exist first, then research studies are done, indicating how effective they are compared to a control group. 

In fields like math instruction, where there is relatively little research, it may mean there are many instructional approaches that just don’t have any existing research on them to let us know whether they are effective or not. 

So while we want to utilize existing research demonstrating methods that are effective and those that are not, we also should not automatically exclude methods that do not yet have research.

Here’s the thing: Nothing has research… until it does. Until someone decides to do a high-quality study on it, demonstrating its efficacy or lack thereof. Then we can make more informed choices about that method.

So what does the research say about effective math instruction?

Websites for Evidence-Based Math Practices

To begin, it is helpful to recognize there are several websites that summarize existing math interventions and research-based approaches. In “Taking the Guesswork out of Locating Evidence-Based Practices for Diverse Learners,” Hughes et al. (2016) provided several options for locating evidence-based practices (EBPs):

A variety of resources summarize and address the most salient features of existing research:

• High-Leverage Practices for Students with Disabilities – Council for Exceptional Children
• Forward Together: A School Leader’s Guide to Creating Inclusive Schools – National Center for Learning Disabilities and Understood.org
• Practice Guide: Assisting Students Struggling with Mathematics: Response to Intervention for Elementary and Middle School – Institute of Educational Sciences

High-Leverage and Evidence-Based Math Practices

In the field of research on math instruction, there are two practices that have the most research:

• Explicit, systematic instruction
• Word problem instruction, specifically using two methods:
  • Attack strategies based on Cognitive Strategy Instruction (CSI) – (Attack strategies consist of a series of steps – or a “plan of attack” – to follow when solving word problems)
  • Schema-Based Instruction (SBI), particularly with an emphasis on transfer to novel situations (SBTI). (Schema-based instruction is a method that helps students solve word problems by teaching them that there are word problem types, and to identify the underlying structure or “schema” of each type)

Forward Together identified four practices for Evidence-Based Math Instruction:

• Explicit instruction with cumulative practice
• Visual representations
• Schema-based instruction
• Peer interaction

There are other practices that have strong research demonstrating their effectiveness:

• Math fact fluency practice and instruction
• Screening students for potential math difficulties and providing interventions

Currently, the Science of Math conversations focus mostly on those practices that have existing research: explicit instruction, attack strategies and schema-based instruction for word problems, use of visual representations, and fluency practice.

The Missing Piece: Subitizing in Math Research

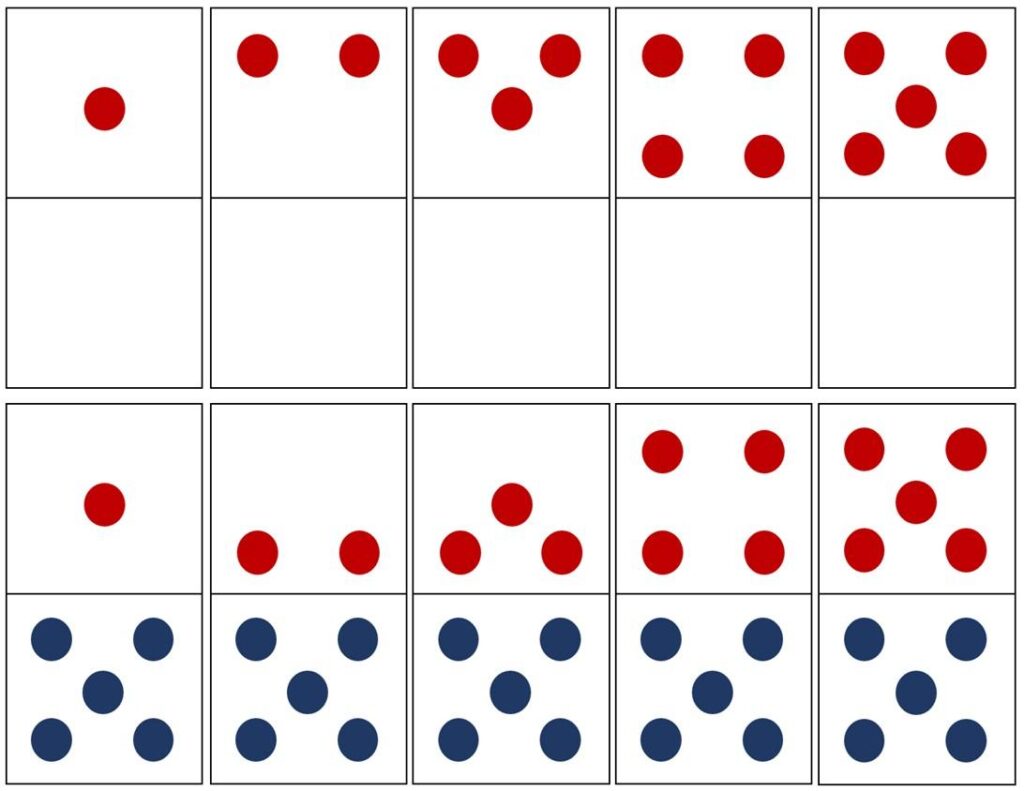
What I couldn’t help but notice was missing from educational research was anything about subitizing. Yet, there is a significant body of research within neuroscience and developmental psychology about the existence of our innate subitizing abilities.

Here is a snapshot of some existing research on subitizing and groupitizing:

• Subitizing: What Is It? Why Teach It?
• Subitizing is sensitive to the arrangement of objects
• Effects of Daily Practice on Subitizing, Visual Counting, and Basic Arithmetic Skills
• Groupitizing reflects conceptual developments in math cognition and inequities in math achievement from childhood through adolescence

In addition to this body of research, I also knew from my extensive work in the field of dyscalculia that developing subitizing and groupitizing using dot patterns is THE foundation and effective remediation for developing number sense and math fact knowledge, particularly in students with dyscalculia and math learning difficulties. 

Expanding the Science of Math Conversation

I parallel developing our subitizing and groupitizing abilities – in order to develop number sense and learn math facts – to developing phonemic awareness and phonics in order to learn to read.

Imagine discussing the Science of Reading and Structured Literacy, but saying nothing about phonemic awareness or phonics. 

What would we be left with? Explicit, systematic instruction… but in what?

I believe that our Science of Math conversations should pull from what we know from research to be effective and not effective, while ALSO exploring methods that are currently being used very successfully for students with dyscalculia. 

We need to open up our discussions to include the emerging fields of neuroscience, psychology, and number sense, and focus not just on the past methods that we already have research on, but also what do we need to get new research on?

Let’s expand our vision to create a model for effective math instruction that doesn’t just address the how – explicit, systematic instruction – but also the what? What should that explicit instruction be on, in order for students to develop strong number sense? And then, the when? When is it developmentally appropriate to teach each component? And last, the how – how do we actually provide and implement this instruction?

Just as the Science of Reading has led to Structured Literacy, a model for effectively teaching literacy based on research and evidence-based practices, the Science of Math needs to lead toward Structured Numeracy – a model for effectively teaching numeracy based on research and evidence-based practices.

Curious to learn more? Read my blog on Structured Numeracy to see what I believe it entails.

So what do I recommend?

Here’s the Science of Math, in a nutshell:

Provide explicit, systematic instruction, using the best manipulatives and visual representations, in:

• Subitizing and Groupitizing: to develop number sense and math facts
• Schema-Based Instruction and Attack Strategies: to develop problem-solving and conceptual understanding of the operations and their relationships

Then provide frequent, interleaved opportunities for practice over time to develop fluency.

---

Introducing the Mathemagical™ Structured Numeracy Curriculum

The Mathemagical™ Structured Numeracy: K-2 Curriculum is designed to align math instruction with the Science of Math. It leverages research-based methods that form and strengthen neural pathways, so every student can develop number sense, math facts, conceptual understanding, and problem-solving skills.
 

We know from research that the most effective math instruction includes explicit, systematic teaching, visual representations, schema-based instruction, and cumulative practice. But there’s a crucial missing piece—subitizing and groupitizing.

Just as phonemic awareness is the foundation of literacy, subitizing is the foundation of numeracy—yet it has been largely overlooked in math education. Mathemagical™ corrects this gap, ensuring that students develop strong number sense, math fact fluency, conceptual understanding, and problem-solving skills in ways that align with how their brains learn.

It’s not about meaningless practice or memorization; it’s about activating the brain’s learning networks through structured, engaging, and effective instruction.

Why Mathemagical™ Works with the Brain:

🧠 Neuroscience-Backed Instruction – Teaching methods designed to strengthen essential neural connections and support deep learning.

🔍 Explicit + Exploratory Learning – Combining structured instruction with hands-on, discovery-based experiences for deeper understanding.

🔢 Structured Numeracy Strategies – Systematic, multisensory math instruction on all strategies in an intentional sequence that builds confidence, fluency, and problem-solving skills.

📚 The Missing Link: Subitizing & Groupitizing – Unlike traditional curriculums, Mathemagical™ directly teaches these foundational skills, ensuring true number sense and numeracy development.

The result? A brain-friendly approach to math that empowers educators and helps students build lasting numeracy skills, math confidence, and a love for learning.

Mathemagical™ creates math-confident kids:

Mathemagicians who have strong number sense, know math facts, and confidently apply numeracy in their daily lives.