First there was Subitizing, and now there’s… Groupitizing!
We all are born with an innate ability to subitize, which means to see a small amount and instantly know how many it is, without counting. One of the most important and transformational ideas I want to get out into math education is that this subitizing ability can be and MUST be the foundation for how we develop number sense and math facts – NOT counting.
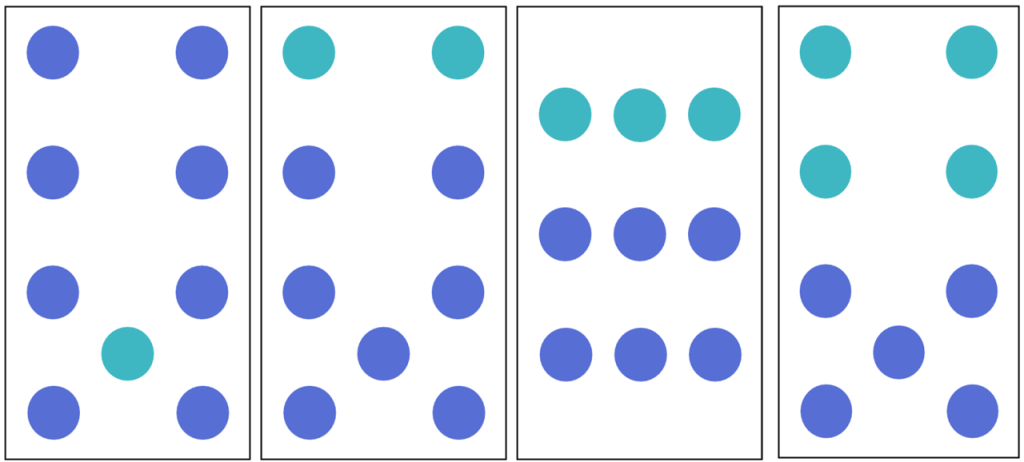
Our innate ability to subitize, however, only extends to about 4 items, possibly 5 when arranged into easy-to-subitize patterns. So to move beyond these smaller numbers, students must be able to combine two or more “subitizable” amounts to determine how many there are in all. I’ve mostly described these two abilities with the language used by Douglas Clements: “perceptual subitizing” is our innate ability to subitize up to about 4 items; “conceptual subitizing” is our ability to combine these groups.
That is… until now. Recently I was listening to a training with Jo Boaler and she referenced recent research on our ability to “groupitize”. Aha! I love it – a new, very catchy word, that beautifully sums up how we can subitize to group amounts and determine larger quantities WITHOUT needing to count. The researchers write:
We investigate the “Groupitizing” ability in 1,209 third to eighth graders (mean age at first timepoint = 10.48, 586 girls, 39.16% Asian, 28.88% Hispanic/Latino, 18.51% White), a process that captures the ability to use grouping cues to access the exact value of a set. Groupitizing improves each year from late childhood to early adolescence (d = 3.29), is a central predictor of math achievement (beta weight = .30), is linked to conceptual processes in mathematics (minimum d = 0.69), and helps explain the dynamic between the ongoing development of non-symbolic number concepts, systemic educational inequities in school associated with SES, and mathematics achievement (minimum beta weight = .11) in ways that explicit symbolic measures may miss.
The statements these researchers make about the effects of “groupitizing” and the correlation to math achievement is profound. The results match what I’ve seen from using these methods with students for years, after I learned about it from practioners working effectively with those who have dyscalculia.
First, let’s recognize that this subitizing and groupitizing approach to instruction has existed for decades – and yet somehow has not made it into mainstream education. I first learned about it from Mahesh Sharma, who uses his Visual Cluster Cards to teach the combinations for all numbers 1-10, based on our innate ability to subitize and groupitize.
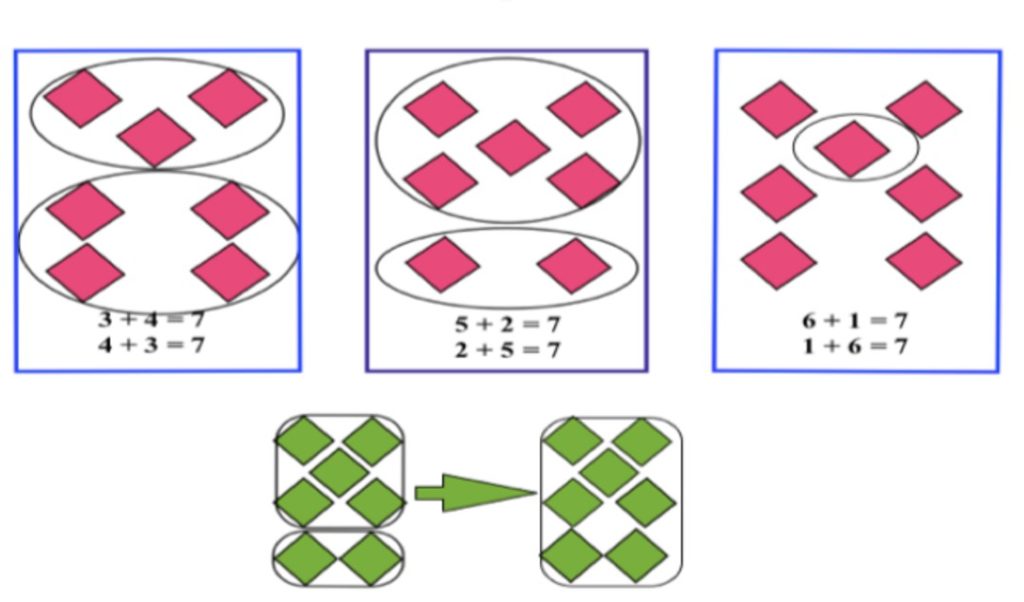
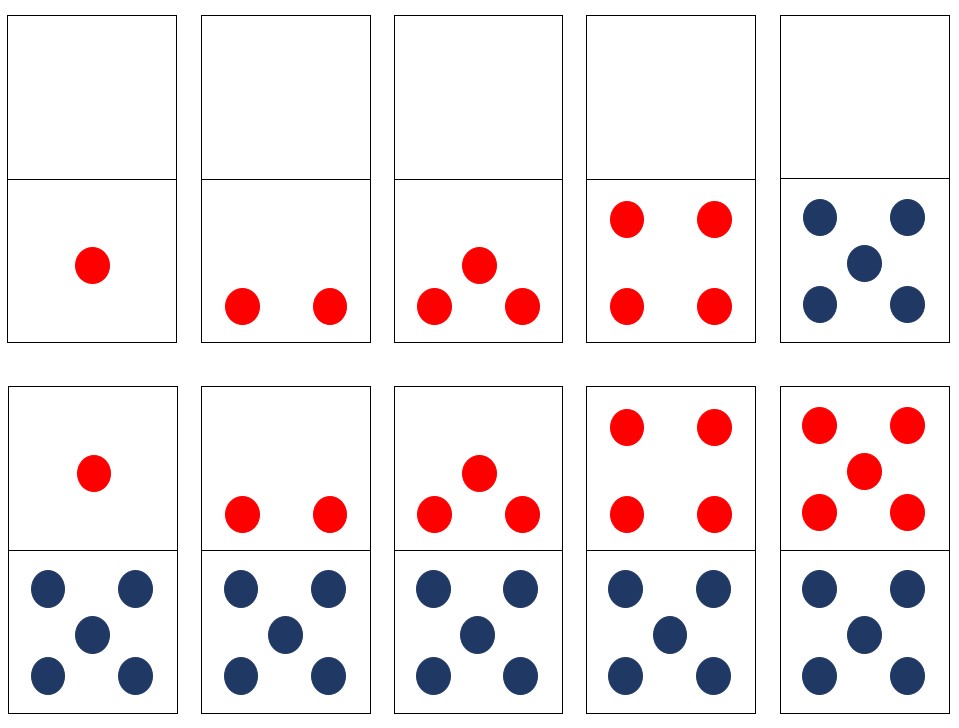
Then several years later, when I saw Chris Woodin’s dot icons, I recognized the brilliance in how he combined red and blue dot patterns to help kids see 5-groups, learn the combinations for 5, then build on these same patterns to groupitize numbers 6-10 and learn the combinations for 10. His arrangements also facilitate kids learning doubles, near doubles, and essential strategies for addition and subtraction like making 10 to add 9, 8, and 7.
More recently, after reading Brian Butterworth’s brilliant book Dyscalculia: From Science to Education, I connected with Rob Jennings and Cat Eadle at the Dyscalculia Network in the UK. I became aware of the multiple practitioners there who have also been using dot patterns for decades to offer effective remediation for dyscalculia: Steve Chinn, Ronit Bird, Dorian Yeo, Jane Emerson, and Rob and Cat themselves, amongst others.
The effects of using these dot patterns with students is not small. I recently had an experienced math specialist tell me: “The dot cards were transformational for me.” Time and again, educators tell me what a difference dot patterns are making for their students, particularly those who are otherwise not learning effectively with the current math curriculum.
One day I opened Facebook to see a teacher had asked what the best elementary math PD was that people had ever received. Someone who had taken my Decoding Math course commented: “Took this (course) last spring and realized I’ve been teaching math wrong for 20 years. Even my lowest kiddos can do mental math now – so fast they are no longer low.”
Comments like this make my day. It’s why I do what I do! Hearing these results and seeing them myself, time and again, fuels my passion for getting the word out about these effective approaches to teaching math.
There are amazing dyscalculia practitioners out there! My goal is to get their work into mainstream math education, and create the comprehensive solution that schools need to provide effective math instruction for ALL.
Let’s end the math struggles and finally see success for everyone.
If you’d like to learn more, check out my online course Decoding Math and our new Mathemagical Membership and Structured Numeracy lessons, which supports educators in implementing effective K-5 math instruction and interventions.